Hoofdstuk 7 TESTS VAN ÉÉN PARAMETER

7.1 EEN EENVOUDIG STATISTISCH MODEL

In vorig hoofdstuk hebben we de normale verdeling besproken. Impliciet, wanneer we die verdeling gebruiken om gegevens te beschrijven (en er eventueel eenvoudige vragen mee beantwoorden) gaan we ervan uit dat onze dataset genomen is uit een populatie die voldoet aan de normaliteitassumptie. We kunnen hier dus spreken van een (zeer eenvoudig) statistisch model:

\[y_i \sim N(\mu, \sigma^2)\]

De datapunten yi (i: 1 … n) worden dus verondersteld uit een populatie te komen waarvan de frequentieverdeling van het kenmerk een normale verdeling voorstelt met gemiddelde \(\mu\) en standaarddeviatie \(\sigma\). Dit zijn de twee parameters die de locatie en breedte van de verdeling bepalen. Hun exacte waarde is onbekend maar kan geschat worden aan de hand van het steekproefgemiddelde en de spreiding van de steekproef (zie hoger). Het onderscheid tussen de parameters en hun schatters kan in de notaties weergegeven worden door op de schatters een ‘hoedje’ te plaatsen. In dit hoofdstuk gaan we de normale verdeling niet gebruiken om de populatie te beschrijven maar om uitspraken te doen over de parameters. Dit gebeurt in twee stappen. In de eerste plaats moeten er hypotheses opgesteld worden. Daarna kunnen die hypotheses getoetst worden en besluiten geformuleerd.

7.2 OPSTELLEN VAN HYPOTHESEN

In statistische termen start een test altijd met het opstellen van een nul hypothese H0 en een alternatieve hypothese Ha. Stel je wilt nagaan of er gorilla’s voorkomen in de Ardennen. Dan kan je vanuit statistisch oogpunt je hypothese op twee manieren formuleren: er zitten geen gorilla’s in de Ardennen of er zitten wel gorilla’s in de Ardennen. Beide omvatten dezelfde idee, maar slechts 1 van hen kan verworpen worden. De tweede formulering kan je nooit verwerpen. Het is niet omdat je geen gorilla’s gezien hebt, dat ze er niet zitten, of m.a.w., de afwezigheid van bewijsmateriaal is niet hetzelfde als het bewijs van afwezigheid. Daar tegenover staat dat vanaf het moment dat je een gorilla gezien hebt in de Ardennen, je de eerste formulering kan verwerpen: aanwezigheid bewijst het niet afwezig zijn. Op deze manier worden statistische hypotheses geformuleerd. Laten we verder gaan met een meer realistisch voorbeeld. Stel je wilt nagaan of het bedrijf Kellogg’s het juiste gewicht in zijn family packs cornflakes doet, nl. 750g. Je zou dit kunnen nagaan door bv. een lukrake steekproef van cornflakes pakken te kopen, en van elk pak het gewicht bepalen. Onderstaande code simuleert dit in R:

gew<-rnorm(25,m=745,sd=10)

gew

##  [1] 739.6114 770.3098 736.6539 751.7018 736.6380 752.8731 758.7254
##  [8] 747.5037 749.0935 741.5591 750.4234 747.9752 744.3965 749.1570
## [15] 745.2166 736.3694 746.6869 743.6041 739.9728 750.6186 749.8472
## [22] 729.7513 757.7722 727.9693 761.1235

Het geschatte gemiddelde en standaarddeviatie kunnen berekend worden als:

mean(gew)

## [1] 746.6221

sd(gew)

## [1] 9.649719

Op basis van het geschatte gemiddelde zou je in de verleiding kunnen komen om te besluiten dat er te weinig cornflakes in de pakken gedaan wordt. Wat je echter niet mag vergeten is dat we slechts een steekproef genomen hebben, en we dus niet kunnen uitsluiten dat dit een toevallig resultaat is terwijl in werkelijkheid het gemiddelde op populatie niveau niet verschilt van 750g. We moeten dus eerst een hypothese opstellen en dan een statistische test uitvoeren. De hypotheses kunnen op 3 manieren opgesteld worden:

tweezijdige toets: \[H_0: \mu = 750 \;\; vs.\; H_a: \mu \neq 750\]
links eenzijdige toets: \[H_0: \mu \geq 750 \;\; vs. \; H_a: \mu < 750\]
rechts eenzijdige toets \[H_0: \mu \leq 750 \;\; vs. \; H_a: \mu > 750\]

7.3 TOETSEN VAN HYPOTHESE OMTREND ÉÉN POPULATIEGEMIDDELDE

7.3.1 DRIE MANIEREN OM EEN HYPOTHESE TOETS UIT TE VOEREN

Er zijn 3 verschillende manieren om een hypothese te toetsen. Deze drie leiden uiteraard steeds tot dezelfde conclusie. Het principe van hypothese toetsen is dat er nagegaan wordt hoeveel evidentie er is tegen de nulhypothese, of met andere woorden hoe onwaarschijnlijk H0 is. Een eerste manier om dit te doen is door een betrouwbaarheidsinterval op te stellen. We kunnen dit door gebruik te maken van een eigenschap van de normale verdeling, namelijk dat wanneer de verdeling van een variabele normaal is, dan is de verdeling van het geschatte gemiddelde ook normaal (indien \(\sigma\) gekend is!):

\[\hat\mu \sim N(\mu, \frac{\sigma}{\sqrt{n}})\]

\(\frac{\sigma}{\sqrt{n}}\) is hier dus de standaard fout.

We weten ook dat 95% van de oppervlakte van een standaard normaal verdeling zich tussen ruwweg-2σ en +2σ bevindt. Het is exacter om te stellen dat 95% van de oppervlakte zich tussen-1.96σ en +1.96σ bevindt. Bovenstaande normale verdeling kan gemakkelijk omgevormd worden tot een standaard normale verdeling als volgt:

\[\frac{\hat\mu-\mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0,1)\] Wanneer we dit 95% interval weergeven geeft dat:

\[P[-1.96<\frac{\hat\mu-\mu}{\frac{\sigma}{\sqrt{n}}} <1.96] = 0.95\] Om tot een 95% interval van \(\mu\) te komen (het zgn. 95% betrouwbaarheidsinterval) Kunnen we deze formule vrij eenvoudig omvormen door eerst alle leden te vermenigvuldigen met \(\sigma\):

\[P[-1.96\frac{\sigma}{\sqrt{n}}<\hat\mu-\mu<1.96\frac{\sigma}{\sqrt{n}}] = 0.95\]

Van elk deel \(\hat\mu\) af te trekken:

\[P[-1.96\frac{\sigma}{\sqrt{n}}-\hat\mu<-\mu<1.96\frac{\sigma}{\sqrt{n}}-\hat\mu] = 0.95\] En elk deel te vermenigvuldigen met -1:

\[P[1.96\frac{\sigma}{\sqrt{n}}+\hat\mu>-\mu>-1.96\frac{\sigma}{\sqrt{n}}+\hat\mu] = 0.95\] \[P[\hat\mu-1.96\frac{\sigma}{\sqrt{n}}<\mu< \hat\mu +1.96\frac{\sigma}{\sqrt{n}}] = 0.95\]

Op deze manier kan een (tweezijdig) betrouwbaarheidsinterval voor \(\mu\) opgesteld worden. De interpretatie van dit interval is (ruwweg) dat we voor 95% zeker zijn dat de werkelijke waarde van \(\mu\) tussen de onder- en de bovengrens ligt. Pas wanneer \(\mu_0\) buiten dit interval ligt wordt \(H_0\) verworpen.

Deze methode is enkel van toepassing als \(\sigma\) gekend is. Wanneer we \(\sigma\) niet kennen en ook moeten schatten (wat meestal het geval is), dan mogen we geen gebruik maken van de standaard normaal verdeling maar moet de t-verdeling toegepast worden.

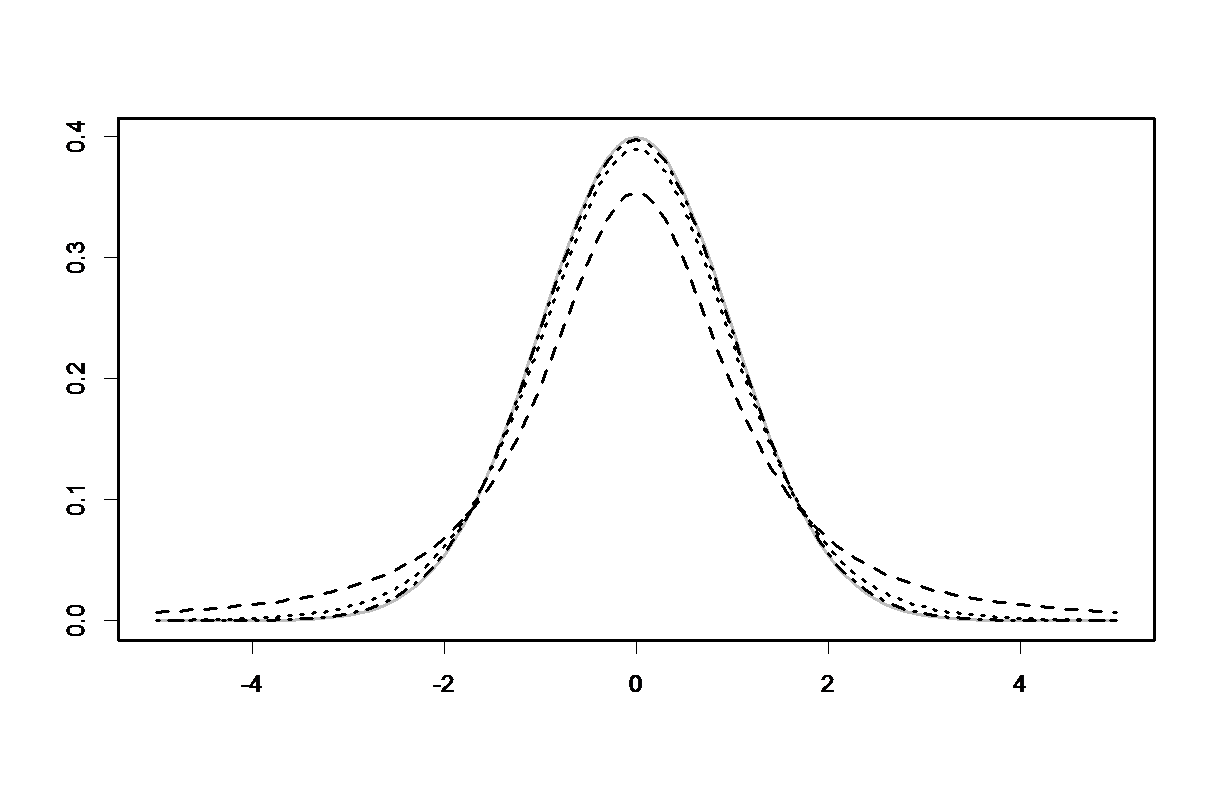
Een t-verdeling ziet er vrijwel hetzelfde uit als een standaard normaal verdeling, behalve dat de staarten een beetje ‘dikker’ zijn. De vorm van de t-verdeling hangt af van het aantal vrijheidsgraden, welke gelijk zijn aan n-1 voor deze methode. In bovenstaande figuur zie je de standaard normaal verdeling (grijs) en enkele t-verdelingen met resp. 2, 10 en 50 vrijheidsgraden. Naarmate dat het aantal vrijheidsgraden (en dus de steekproefgrootte) groter worden, komt de t-verdeling dichter bij de standaard normaal verdeling te liggen.

De kwantielen van de t-verdeling kunnen in R berekend worden per de functie qt(kwantiel, vrijheidsgraden), of opgezocht worden in een tabel (zie appendix).

Het 95% betrouwbaarheidsinterval voor het gemiddelde moet dan als volgt berekend worden:

\[P[\hat\mu+t_{0.025,n-1}\frac{\hat\sigma}{\sqrt{n}}<\mu< \hat\mu +t_{0.975,n-1}\frac{\hat\sigma}{\sqrt{n}}] = 0.95\] Voor de eenzijdige toetsen wordt enkel de boven (links-eenzijdig) of de ondergrens (rechts-eenzijdig) grens berekend:

\[P[-\infty <\mu< \hat\mu +t_{0.95,n-1}\frac{\hat\sigma}{\sqrt{n}}] = 0.95\] \[P[\hat\mu +t_{0.05,n-1}\frac{\hat\sigma}{\sqrt{n}}<\mu<+\infty ] = 0.95\] De tweede en derde manier om hypothesen te toetsen zijn gebaseerd op de zgn. T-statistiek:

\[T=\frac{\hat\mu-\mu_0}{\frac{\hat\sigma}{\sqrt{n}}}\]

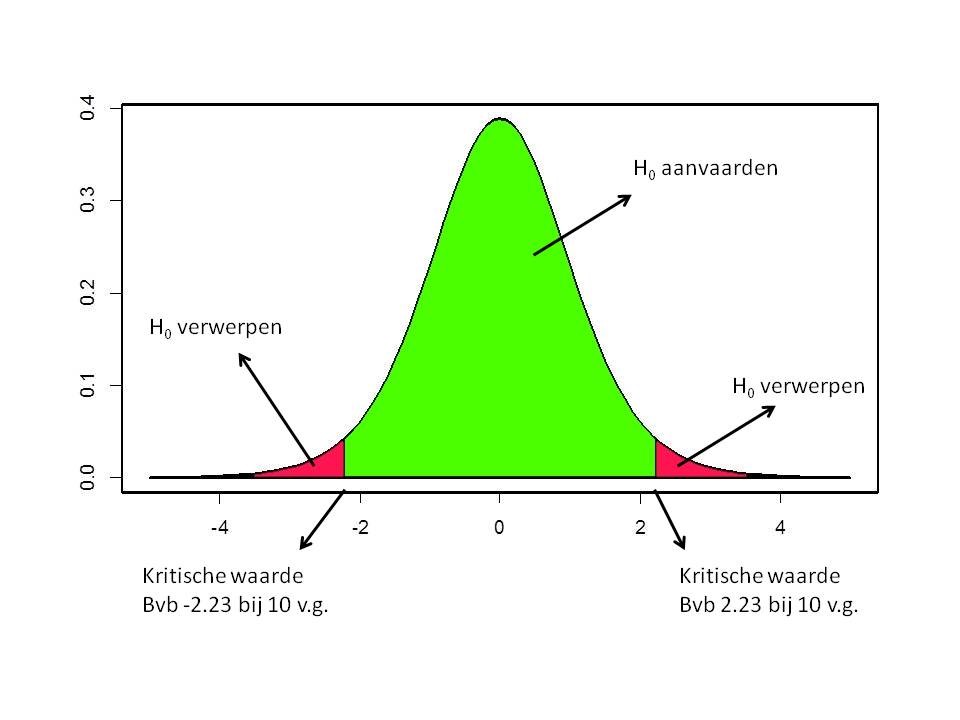
Deze volgt een t-verdeling met n-1 vrijheidsgraden wanneer H0 correct is. Het is dan mogelijk om deze t-verdeling in te delen in een aanvaardingsregio en een verwerpingsregio. Voor tweezijdige tests worden de grenzen van deze regio gegeven door \(t_{0.025,n-1}\) en \(t_{0.975,n-1}\). Voor eenzijdige tests wordt, zoals bij het opstellen van betrouwbaarheidsintervallen de grens gegeven door \(t_{0.05,n-1}\) of \(t_{0.95,n-1}\).

We kunnen dit als volgt grafisch voorstellen voor een tweezijdige tests:

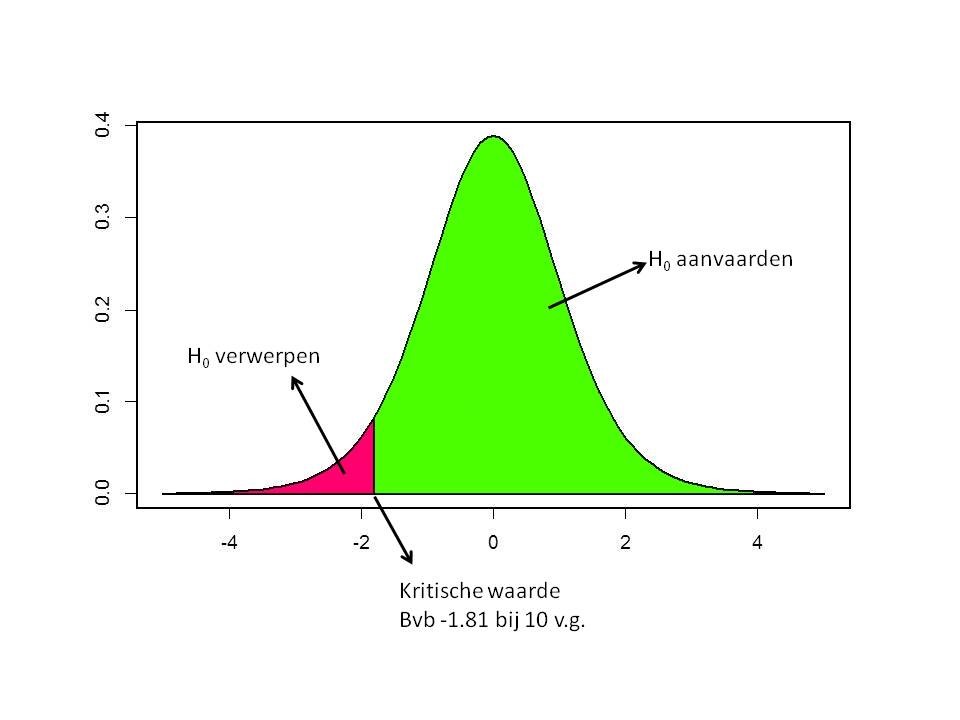
Voor bv. een links-éénzijdige tests geeft dat:

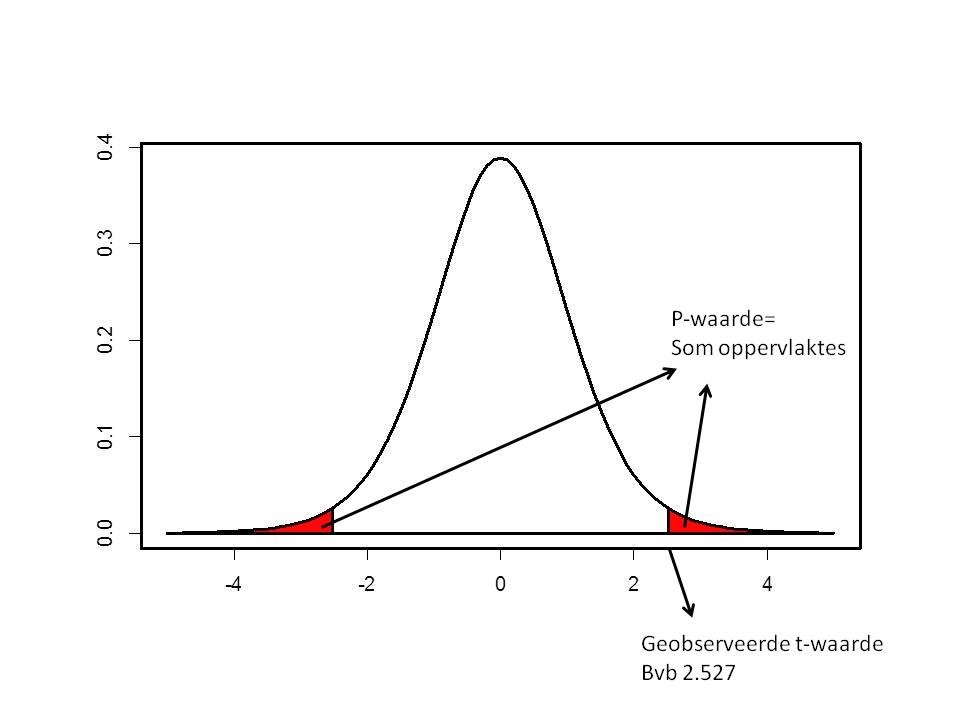
Tot slot, en veruit het vaakst toegepast, kunnen hypotheses ook getoetst worden via een z.g. p-waarde. De berekende waarde voor T wordt dan niet vergeleken met een kritische waarde, maar de kans om een extremer resultaat te bekomen (wanneer H0 waar is) wordt berekend op basis van de t-verdeling:

7.3.2 HET VOORBEELD VAN DE CORNFLAKES DATA

Laten we bovenstaande principes toepassen op de data die we gegenereerd hebben voor de cornflakes data. Laten we beginnen met de tweezijdige toets. We nemen de uitgangspositie in dat we in beide richtingen van verschil geïnteresseerd zijn en stellen de hypothesen als volgt op:

\[H_0: \mu = 750 \;\; vs.\; H_a: \mu \neq 750\]

Met behulp van de functie t.test worden alle noodzakelijke berekeningen uitgevoerd:

(ttest<-t.test(gew, mu = 750))

## 
##  One Sample t-test
## 
## data:  gew
## t = -1.7502, df = 24, p-value = 0.09285
## alternative hypothesis: true mean is not equal to 750
## 95 percent confidence interval:
##  742.6389 750.6054
## sample estimates:
## mean of x 
##  746.6221

De meest relevante waarden zijn de teststatistiek t = -1.7502, de vrijheidsgraden df = 24 en de p-waarde p = 0.0929. De p-waarde geeft kort gezegd de kans weer dat \(H_0\) waar is. Een eerste manier om \(H_0\) te testen is door naar het betrouwbaarheidsinterval te kijken. Dit bevat 750, zodat we \(H_0\) aanvaarden. We kunnen ook de teststatistiek bekijken. Die is gelijk aan -1.7502 terwijl de kritische waarde gegeven wordt door -2.064:

qt(0.025, 24)

## [1] -2.063899

Ook hier besluiten we om \(H_0\) te aanvaarden. En tot slot blijkt natuurlijk ook dat de p-waarde groter is dan 5%.

Een manier om dit kort maar volledig te verwoorden is: We voeren een tweezijdige t-test uit en gaan na of de gemiddelde hoeveelheid corn flakes gelijk is aan 750g. Gemiddeld bevatten de 25 cornflakes pakken 746.6g cornflakes (95% betrouwbaarheidsinterval: 742.6 – 750.6). Dit blijkt echter niet significant te verschillen van 750g (\(t_{24} =-1.75\), \(p=0.093\)). Er is dus niet voldoende evidentie ervan uit te gaan dat er minder dan 750 g cornflakes in de pakken zit.

In dit specifieke geval is het misschien logischer om een éénzijdige toets uit te voeren. We zijn namelijk vooral geïnteresseerd in de vraag of er wel voldoende cornflakes in de pakken gedaan wordt. Hier spreken we dan van een links-eenzijdige toets waarbij we de hypotheses als volgt opstellen:

\[H_0: \mu \geq 750 \;\; vs. \; H_a: \mu < 750\]

De test in R kan als volgt toegepast worden:

t.test(gew,mu=750,alternative='less')

## 
##  One Sample t-test
## 
## data:  gew
## t = -1.7502, df = 24, p-value = 0.04643
## alternative hypothesis: true mean is less than 750
## 95 percent confidence interval:
##      -Inf 749.9241
## sample estimates:
## mean of x 
##  746.6221

We stellen nu vast dat \(H_0\) wel verworpen kan worden. Het is belangrijk te weten dat de keuze om een éénzijdige of tweezijdige toets uit te voeren a priori genomen moet worden, en niet mag afhangen van de data zelf!

Voor een rechts-eenzijdige toets (wat hier weinig zinvol is) kan de test als volgt uitgevoerd worden:

\[H_0: \mu \leq 750 \;\; vs. \; H_a: \mu > 750\]

t.test(gew,mu=750,alternative='greater')

## 
##  One Sample t-test
## 
## data:  gew
## t = -1.7502, df = 24, p-value = 0.9536
## alternative hypothesis: true mean is greater than 750
## 95 percent confidence interval:
##  743.3202      Inf
## sample estimates:
## mean of x 
##  746.6221

Tot slot is het ook belangrijk om de normaliteit van de gegevens te checken, en dat blijkt hier niet voor problemen te zorgen:

hist(gew)

shapiro.test(gew)

## 
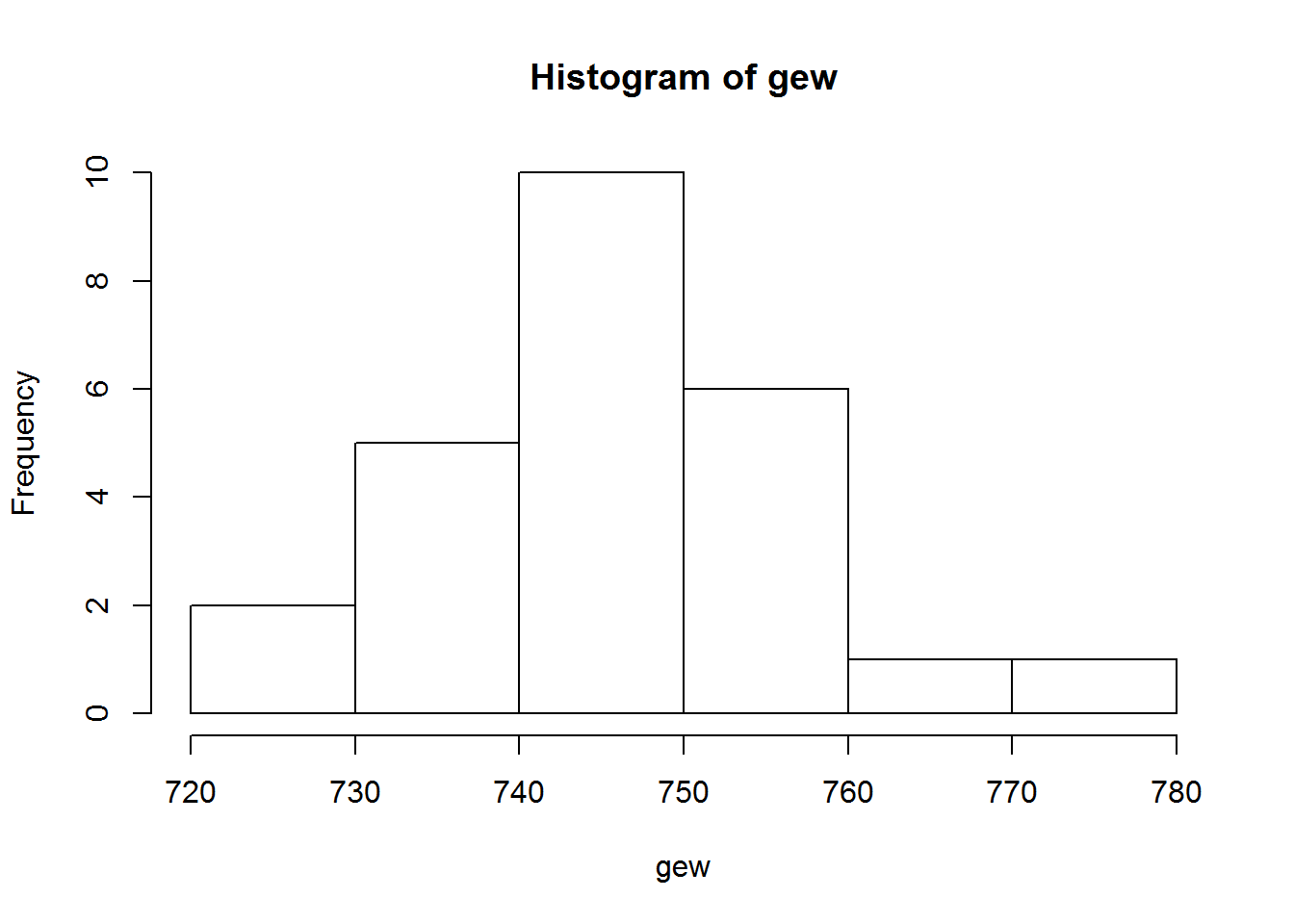
##  Shapiro-Wilk normality test
## 
## data:  gew
## W = 0.98019, p-value = 0.8888

7.4 NIET-PARAMETRISCHE TEST

Bovenstaande test noemen we de one-sample t-test. Deze methode start vanuit de assumptie dat de gegevens uit een populatie komen waarvoor normaliteit opgaat. Dit is niet noodzakelijk het geval. In het geval van afwijkingen van normaliteit zijn er drie mogelijke pistes te volgen.

Wanneer de steekproefgrootte voldoende groot is (>50) kunnen we ons beroepen op de centrale limietstelling. Deze stelt dat, wanneer een steekproef genomen wordt uit een populatie die niet voldoet aan de normale verdeling, dat wanneer de steekproefgrootte voldoende hoog is de verdeling van het gemiddelde toch benaderd kan worden door een normale (of t-) verdeling. Met andere woorden, als de steekproefgrootte voldoende hoog is hoeven we ons geen zorgen te maken van afwijkingen van normaliteit.
Een alternatieve oplossing is om een transformatie te vinden om de verdeling de normale verdeling te laten benaderen. Zo is het vaak het geval dat gewichten of concentraties een lognormale verdeling volgen. Het nemen van een natuurlijk logaritme kan dan nuttig zijn. Verder in de cursus zullen we ook de zgn. Box-Cox power transformaties illustreren
Als derde mogelijkheid kan er gebruik gemaakt worden van de zgn. niet-parametrische tests. Het verschil met parametrische tests is dat er geen veronderstellingen gemaakt worden met betrekking tot een verdeling EN de hypothese niet langer in termen van een parameter geformuleerd wordt. Als niet parametrisch alternatief voor het gemiddelde kunnen we gebruik maken van de mediaan. Als \(H_0\) waar is, dan is de verwachting – op basis van de definitie van de mediaan – dat de verwachte waarde in het midden van de data ligt. De meest eenvoudige test is de teken test. Hierbij gaan we het probleem herleiden tot een test voor proporties. We kunnen bv. tellen hoe vaak het gewicht boven 750 lag. Als \(H_0\) waar is zou dat moeten overeen komen met 50% (hier dus 12 à 13 keer):

gew>750

##  [1] FALSE  TRUE FALSE  TRUE FALSE  TRUE  TRUE FALSE FALSE FALSE  TRUE
## [12] FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE
## [23]  TRUE FALSE  TRUE

som<-sum(gew>750)
som

## [1] 8

In werkelijkheid waren slechts 8 van de 25 waarnemingen groter dan 750. Met behulp van de binomiale verdeling kunnen we dan snel nagaan of 8 successen op een totaal van 25 significant verschilt van 50%:

binom.test(som,25,0.5)

## 
##  Exact binomial test
## 
## data:  som and 25
## number of successes = 8, number of trials = 25, p-value = 0.1078
## alternative hypothesis: true probability of success is not equal to 0.5
## 95 percent confidence interval:
##  0.1494954 0.5350007
## sample estimates:
## probability of success 
##                   0.32

Dit blijkt niet het geval te zijn.

De teken test is echter een erg ruwe test waarbij de continue data naar een ja/nee (binaire) variabele wordt omgezet. Een beter en krachtiger alternatief is de Wilcoxon test. Deze maakt gebruik van de rangordes van de data. We laten de details achterwege en bekijken enkel de manier waarop de test in R uitgevoerd kan worden.

wilcox.test(gew,mu=750)

## 
##  Wilcoxon signed rank test
## 
## data:  gew
## V = 93, p-value = 0.06263
## alternative hypothesis: true location is not equal to 750

7.5 TOETSEN VAN HYPOTHESE OMTREND ÉÉN VARIANTIE

Zoals voor het steekproefgemiddelde is het ook mogelijk om een betrouwbaarheidsinterval op te stellen voor de steekproefvariantie. Hiervoor wordt dezelfde ‘strategie’ gebruikt als voor het gemiddelde, namelijk door gebruik te maken van een verdeling, in dit geval een Chi-kwadraat verdeling. Voor normaal verdeelde data kan aangetoond worden dat:

\[\frac{(n-1)\hat\sigma^2}{\sigma^2} \sim \chi_{n-1}^2\]

Net zoals bij het opstellen van het betrouwbaarheidsinterval voor een gemiddelde kan hieruit een boven en een ondergrens afgeleid worden. Dit geeft het volgende resultaat:

ondergrens: \(\frac{(n-1)\hat\sigma^2}{\chi_{1-\frac{a}{2};n-1}^2}\)

bovengrens: \(\frac{(n-1)\hat\sigma^2}{\chi_{\frac{a}{2};n-1}^2}\)

In R kunnen we dit als volgt berekenen:

v<-var(gew)
#ondergrens:
(24*v)/qchisq(0.975,24)

## [1] 56.77282

#bovengrens:
(24*v)/qchisq(0.025,24)

## [1] 180.2099

En besluiten we dat we voor 95% zeker zijn dat de werkelijke variantie tussen 56.7728228 en 180.2098782 ligt.

7.6 TYPE I, TYPE II FOUTEN EN STATISTISCHE KRACHT (POWER)

In een van de eerste passages van deze cursus wordt vermeld dat met statistiek niets bewezen kan worden en dat er enkel uitspraken gedaan worden in termen van kansen. Dit impliceert dat er dus fouten gemaakt worden en dat het niet mogelijk is om in te schatten wanneer zulke fouten optreden. In relatie tot het toetsen van hypotheses zijn er 4 mogelijke combinaties, waarvan er 2 leiden tot een foute uitspraak. Dit staat in volgende tabel samengevat:

De type I fout komt in \(\alpha\)% van de gevallen voor. Aangezien we \(\alpha\) meestal gelijk stellen aan 5%, kunnen we er dus van uit gaan dat wanneer \(H_0\) juist is (wat we nooit kunnen weten), we deze in 5% van de gevallen foutief gaan verwerpen. Laten we de proef op de som nemen en allemaal onderstaande stukje code laten lopen. Hierbij wordt een dataset van 50 waarnemingen gegenereerd uit een standaard normaal verdeling en dan getest of het gemiddelde al dan niet verschilt van 0 (dus \(H_0\) is waar).

t.test(rnorm(50))

## 
##  One Sample t-test
## 
## data:  rnorm(50)
## t = 0.55523, df = 49, p-value = 0.5813
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -0.2234760  0.3941106
## sample estimates:
##  mean of x 
## 0.08531727

Je zal klassikaal merken dat er in ruwweg 5% van de gevallen toch een p-waarde berekend wordt die kleiner is dan 5%. We kunnen ook nagaan of dit afhangt van de steekproefgrootte of de spreiding op de data, waaruit zal blijken dat dat niet het geval is. Met andere woorden, de kans op een type I fout is altijd gelijk aan \(\alpha\)=5% (of in uitzonderlijke gevallen een andere waarde).

Een tweede soort van fout dat we kunnen maken is \(H_0\) aanvaarden terwijl ze fout is. Dit treedt op in \(\beta\)% van de gevallen. De grootte van \(\beta\) ligt echter niet vast en hangt af van enkele factoren. Op basis van onderstaande figuur kan je afleiden welke factoren \(\beta\) beïnvloeden.

In de eerste plaats hangt \(\beta\) af van het werkelijke verschil tussen \(H_0\) en \(H_a\) . Dit kan direct duidelijk gemaakt worden aan de hand van een voorbeeldje. Wanneer je het gewicht van muizen en olifanten wil vergelijken, dan is het voldoende om 2 olifanten en 2 muizen te wegen, en het verschil zal altijd statistisch significant zijn. Dat is omdat het werkelijke verschil, of het verschil waarin je geïnteresseerd bent zeer groot is.

In de tweede plaats hangt \(\beta\) ook af van \(\alpha\). Dat wordt in de volgende figuur weergegeven:

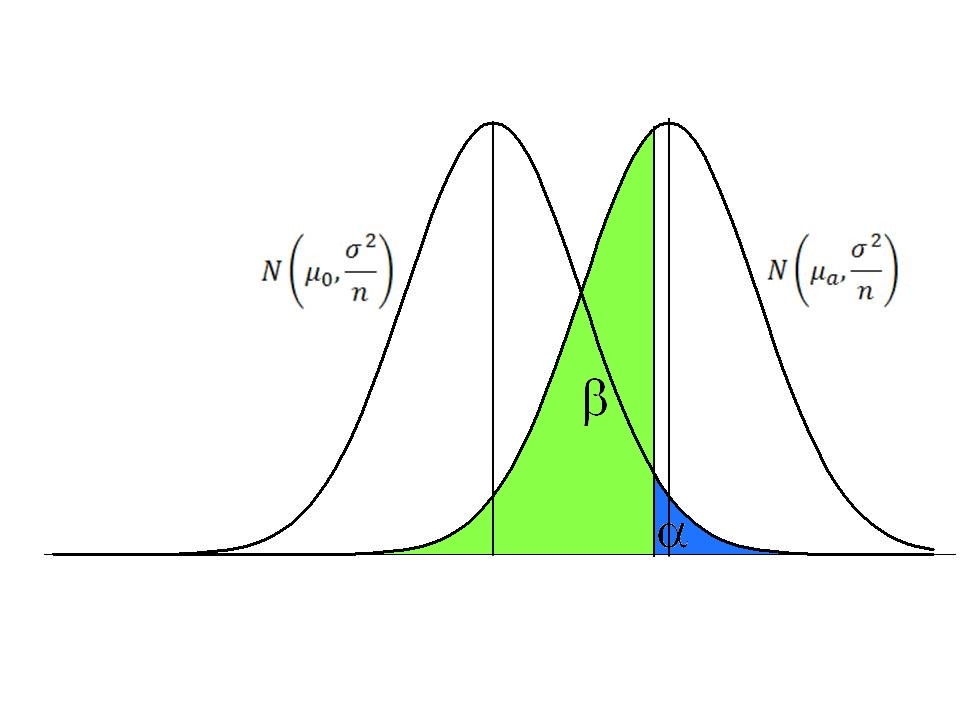
Indien de blauwe oppervlakte kleiner wordt, dan zal de groene oppervlakte toenemen, en omgekeerd. Met andere woorden, als je strenger wilt zijn en een kleinere kans op type I fout neemt (bv. \(\alpha\)=1%) dan ga je automatisch een hogere kans hebben dat je een type II fout maakt. Ook kan je in bovenstaande figuur zien dat wanneer het verschil tussen het verwachte gemiddelde onder \(H_0\) en dat van \(H_a\) groter wordt, \(\beta\) kleiner wordt. Tot slot kan \(\beta\) ook beïnvloed worden door de breedte van de normale verdelingen. Die wordt bepaald door de standaardafwijking (of de variantie) en de steekproefgrootte. Naarmate de standaardafwijking kleiner is en/of de steekproef groter zullen de normale verdelingen in de figuur smaller worden, en zal \(\beta\) ook kleiner worden. In deze gevallen zal 1-\(\beta\), de power of statistische kracht van een test, toenemen.

7.7 OEFENINGEN

Computermodellen voorspellen dat er gemiddeld 10 cm sneeuw ligt op de Kalmthoutse heide met Kerstmis. De metingen van de dikte van de sneeuwlaag van 10 random geselecteerde jaren van de 20ste eeuw zijn: 8, 0, 0, 16, 0, 12, 1, 2, 25, 0 cm. Bevestigen deze gegevens de computervoorspellingen?
Het ideale cholesterol gehalte voor vrouwen van 35 jaar bedraagt 175. Een arts kan gebruik maken van cholesterol gehaltes van 12 vrouwen uit Oost-Vlaanderen: 136, 232, 187, 168, 287, 189, 175, 160, 272, 145, 190, 210.