Hoofdstuk 6 DE NORMAAL VERDELING

6.1 INLEIDING

Zoals aangegeven bij de bespreking van de verschillende types van data, gaan we ons in deze cursus voornamelijk richten op continue data gemeten op een ratioschaal. Terwijl de binomiaal verdeling gebruikt kan worden voor de analyse of beschrijving van binaire data (aan/uit – ja/nee), wordt de normale verdeling zeer frequent gebruikt bij de analyse van continue data. Daar zijn verschillende redenen voor. In de eerste plaats is het zo dat heel wat biologische data goed benaderd kunnen worden door een normale verdeling. Ten tweede, en dat komt verder ook aan bod, stelt de centrale limiet stelling dat wanneer de gegevens niet voldoen aan de normaliteitassumptie, dit bij grote steekproeven (N>50) niet voor problemen zorgt (zie verder). Tot slot heeft de normale verdeling ook het voordeel dat gemiddelde en variantie als twee aparte en onafhankelijke parameters wordt voorgesteld.

\[f(x)=\frac{e^{\frac{1}{2}(\frac{x-\mu}{\sigma})^2}}{\sigma\sqrt{2\pi}}\] We kunnen hier twee Griekse letters (buiten de door iedereen gekende ‘pi’) herkennen, namelijk de mu en de sigma. Mu is de parameter die het gemiddelde of het midden van de normale verdeling weergeeft, sigma is de parameter die de spreiding weergeeft. In onderstaande figuur zie je voorbeelden van enkele normale verdelingen. De volle lijn is wat men de standaard normale verdeling noemt, met een gemiddelde gelijk aan 0 en standaarddeviatie gelijk aan 1. De gestreepte lijn, is een normale verdeling met gemiddelde gelijk aan 2 en standaarddeviatie gelijk aan 1. Tot slot stelt de gestippelde lijn een normale verdeling voor met gemiddelde gelijk aan 0 en standaarddeviatie gelijk aan 0.65. Verschillen in gemiddeldes zijn dus te zien op basis van verschuivingen, verschillen in standaarddeviatie uiten zich in verschillen in de breedte van de verdeling (ook spreiding genoemd).

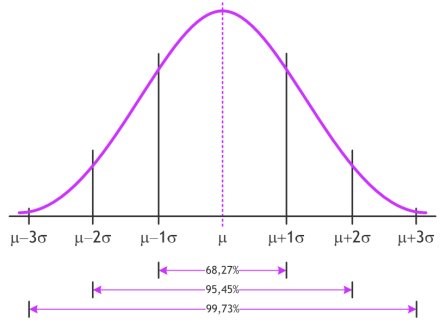
Gemiddelde en standaarddeviatie beschrijven de ligging en breedte van de normale verdeling. De vorm ligt vast. Uit onderstaande figuur kan je afleiden dat ongeveer 68% van de massa onder de normale verdeling (dus 68% van de populatie) zich tussen \(\mu-\sigma\) en \(\mu+\sigma\) bevinden (dit zijn tevens de buigpunten van de normale verdeling). een vaak gebruikt interval (zie ook hoofdstuk over de binomiale verdeling) is het 95% interval. We kunnen vaststellen dat ongeveer 95% van de data tussen \(\mu-2\sigma\) en \(\mu+2\sigma\) bevinden. Een interval tussen \(\mu-3\sigma\) en \(\mu+3\sigma\) bevat 99.7 % van alle data, zodat vaak gesteld wordt dat gegevens die buiten dit interval bevinden als ‘uitzonderlijk’ beschouwd kunnen worden. Men spreekt dan ook van ‘uitbijters’, ‘uitschieters’ of ‘outliers’.

6.2 DE NORMALE VERDELING ALS BESCHRIJVING VAN DE POPULATIE

In het meest eenvoudige geval kunnen we de normale verdeling gaan gebruiken om de verdeling van een variabele te beschrijven en eenvoudige uitspraken te doen over kansen en kwantielen. De mogelijkheden worden hier overlopen aan de hand van een voorbeeld dataset. In het bestand punten_dierkunde.txt vind je de punten op het examen dierkunde van een reeks studenten enkele jaren terug. Om de normale verdeling te kunnen gebruiken als ‘tool’ om de populatie te beschrijven is het noodzakelijk dat de verdeling van de data de normale verdeling benaderen. In een eerste stap gaan we dus enkele figuren maken om dit te bekijken.

Hieronder volgen de boxplots en histogrammen voor zowel theorie als practicum scores:

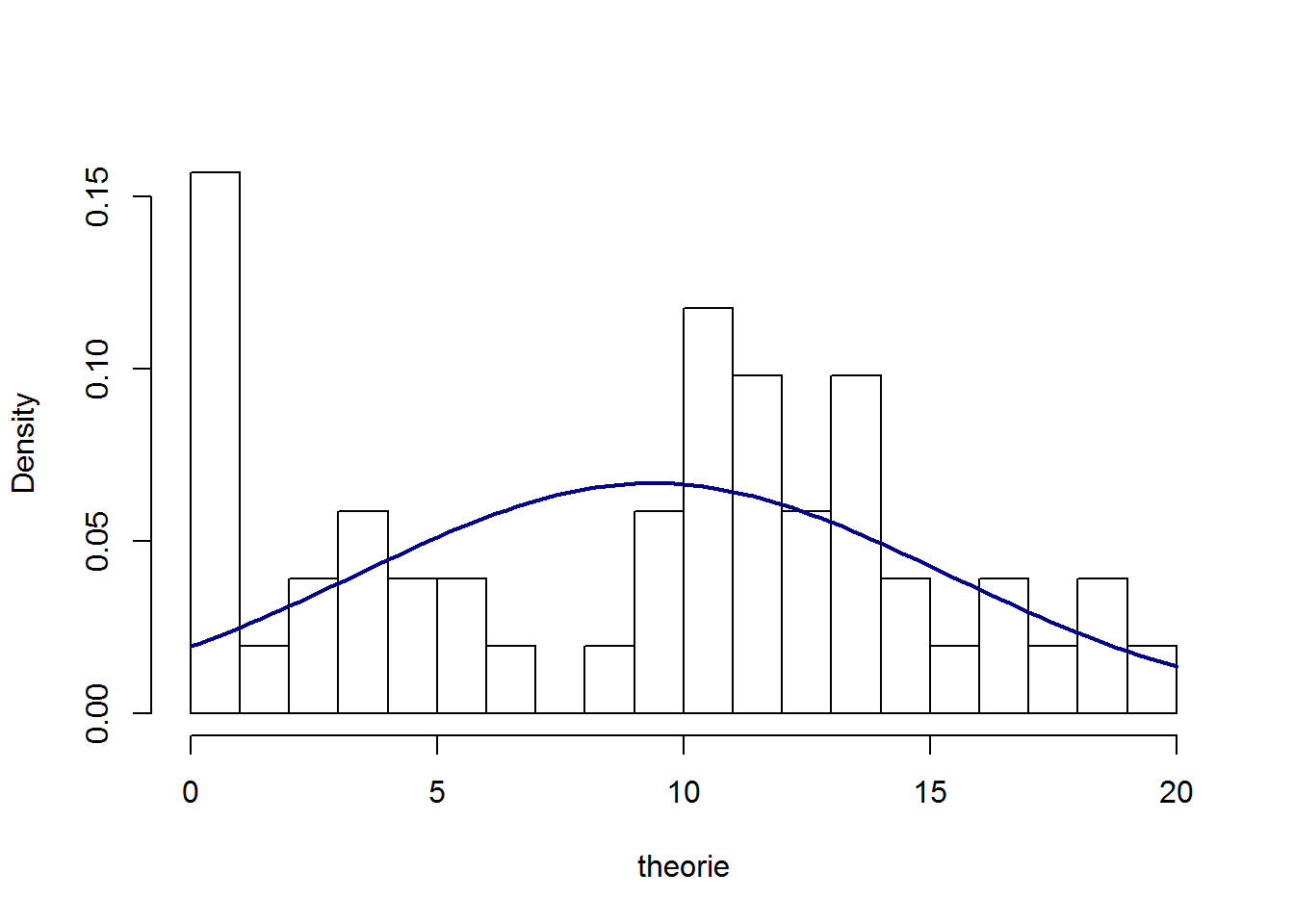
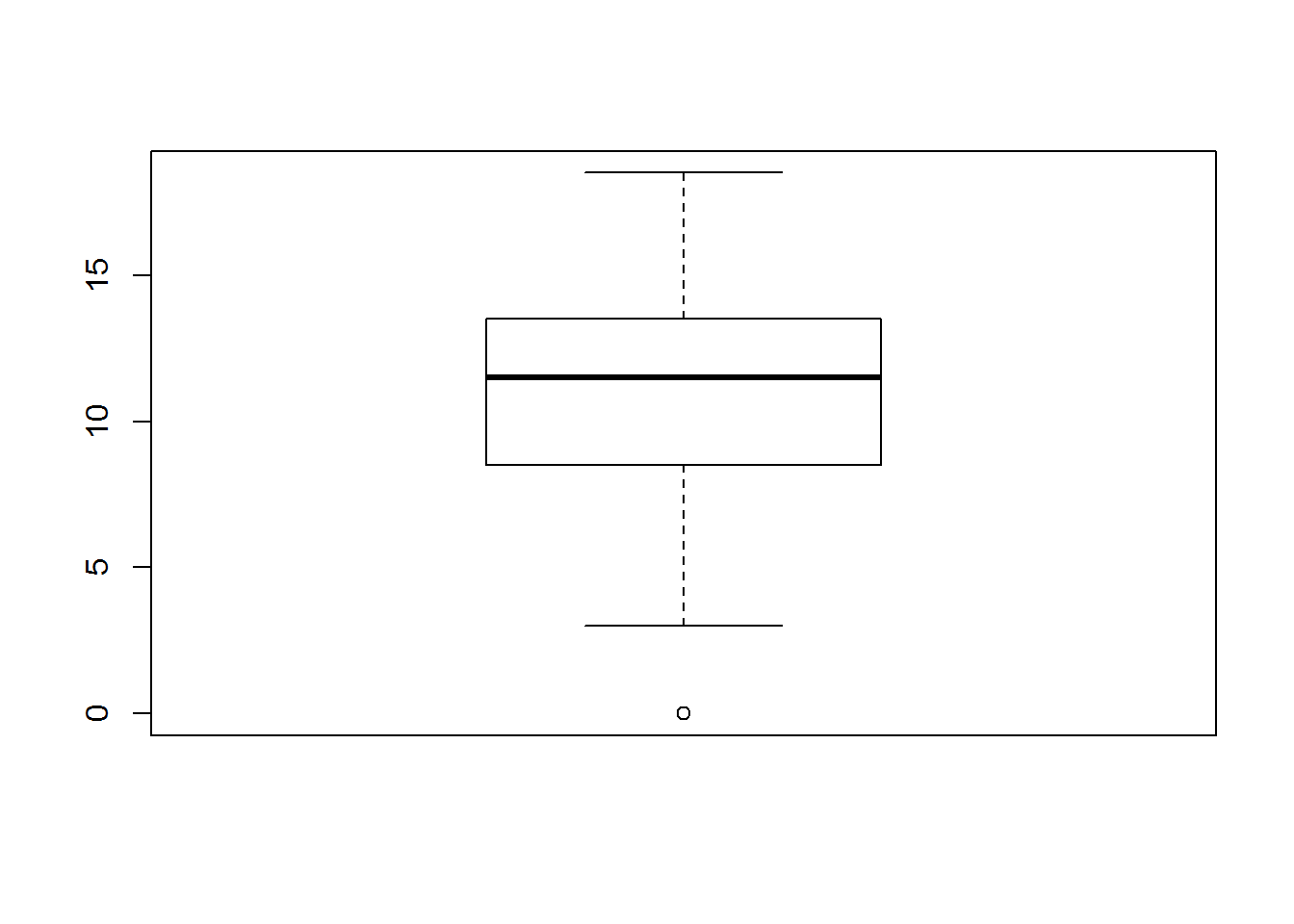
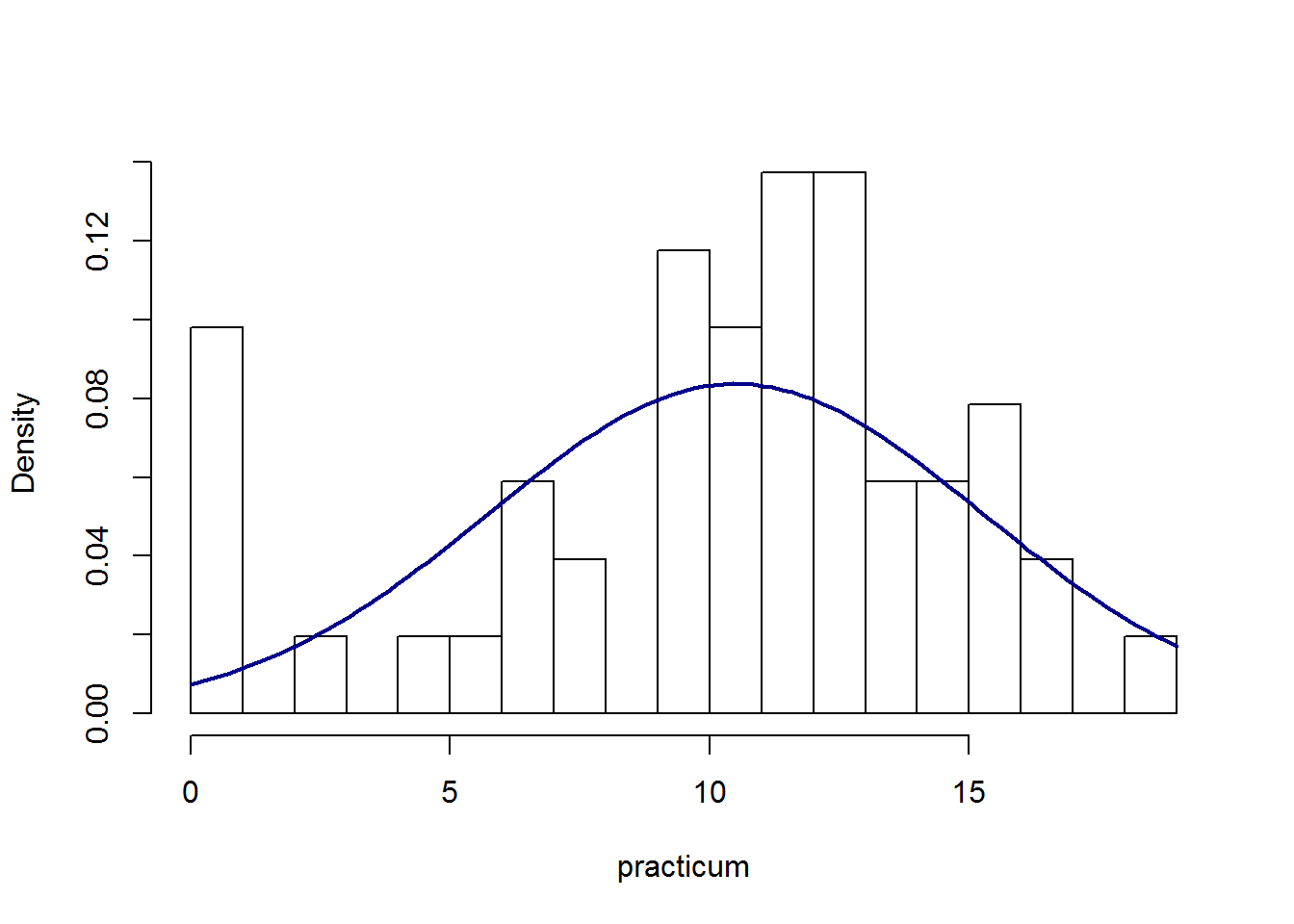In beide gevallen zien we substantiële afwijkingen van normaliteit. Wanneer we de totale score op 20 berekenen en dezelfde figuren bekijken zien we dat de normale verdeling al beter benaderd wordt (maar zeker niet perfect).

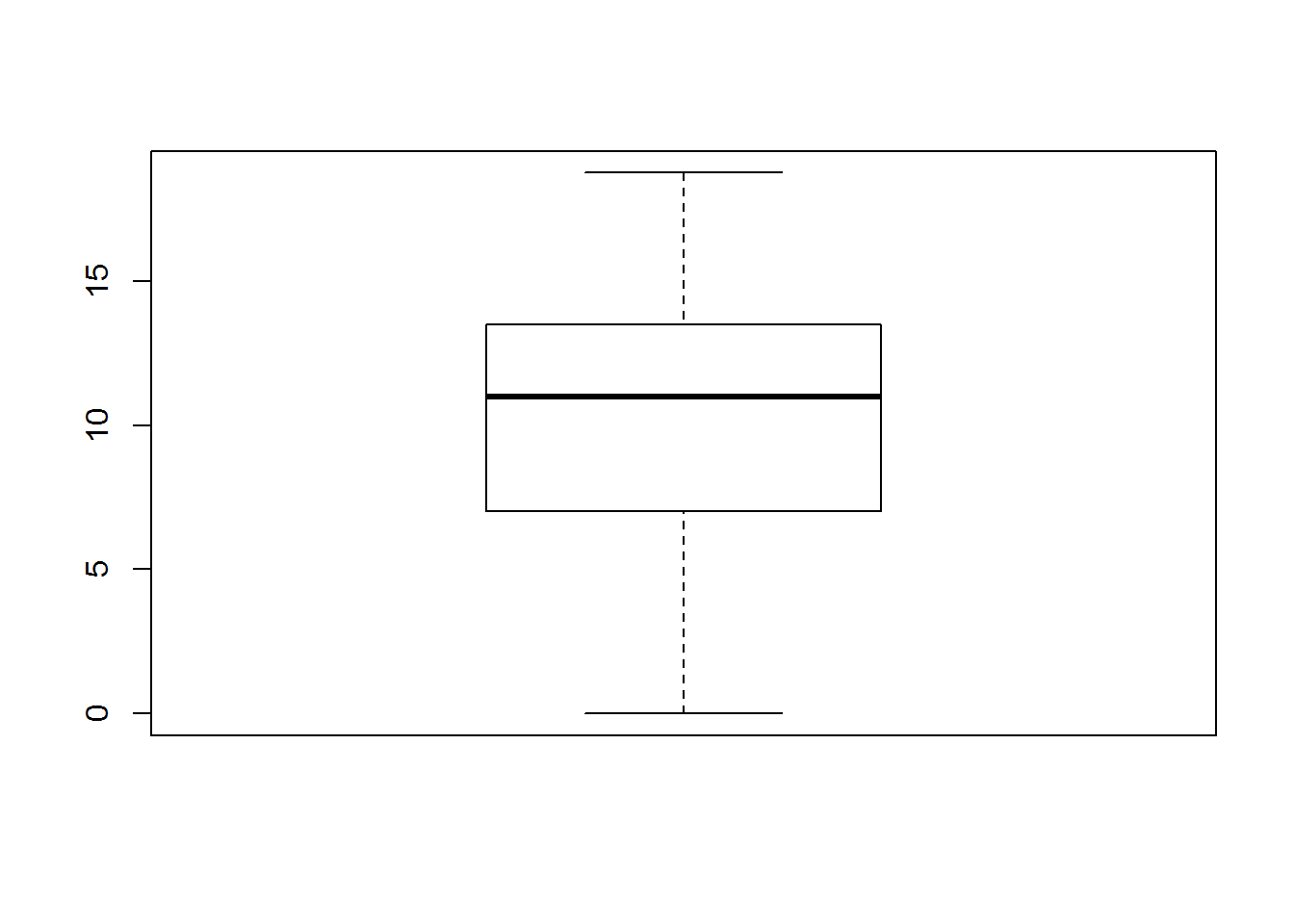
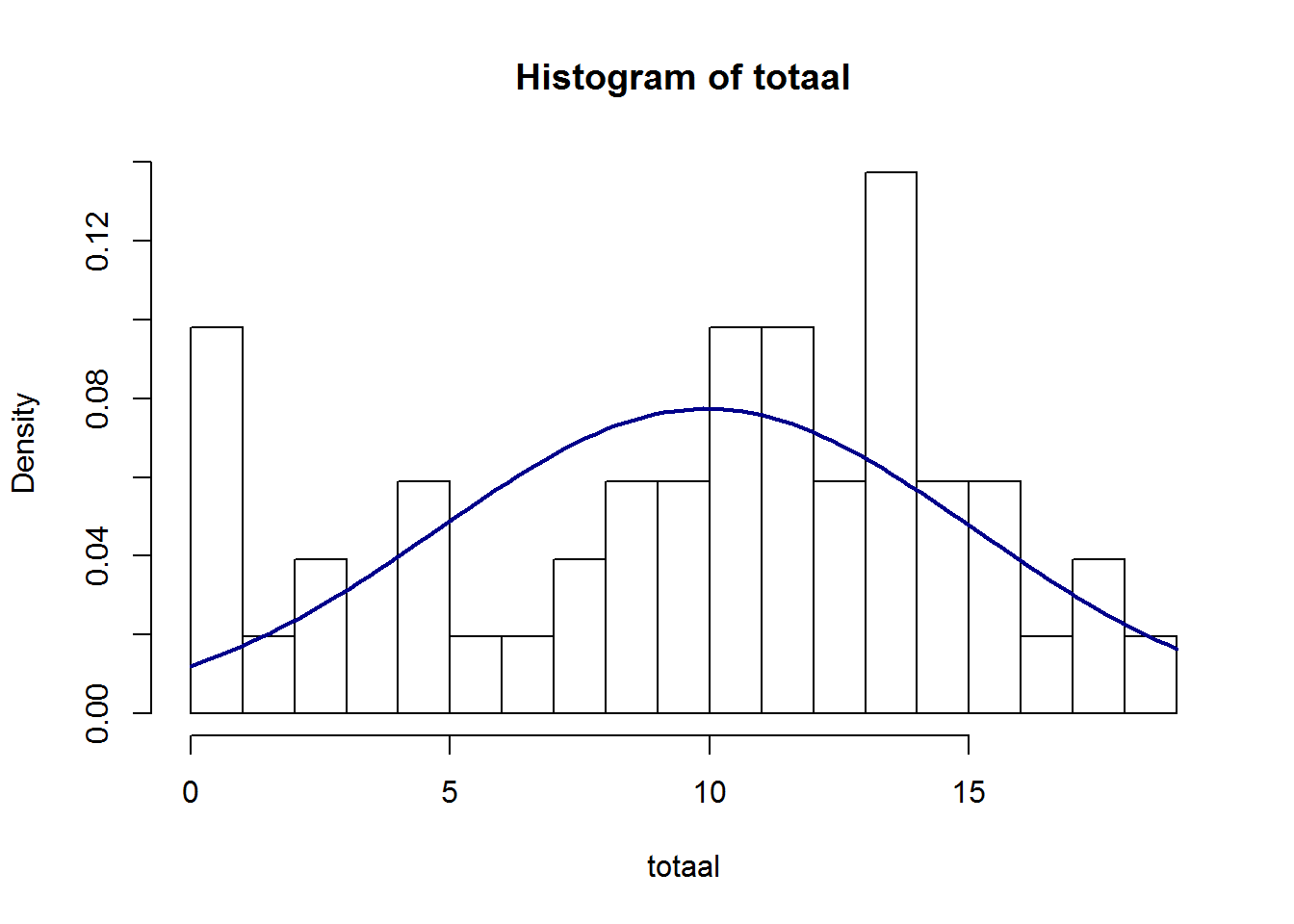
Of het al dan niet geoorloofd is om hier de normale verdeling toe te passen is een keuze die gemaakt moet worden. Er zijn niet altijd eenduidige regels wanneer welke keuze gemaakt moet worden. We gaan hier ervan uit dat de verdeling voldoende overeen komt met een normale verdeling. Het gemiddelde is gelijk aan 9.93, met een standaardafwijking van 5.16.

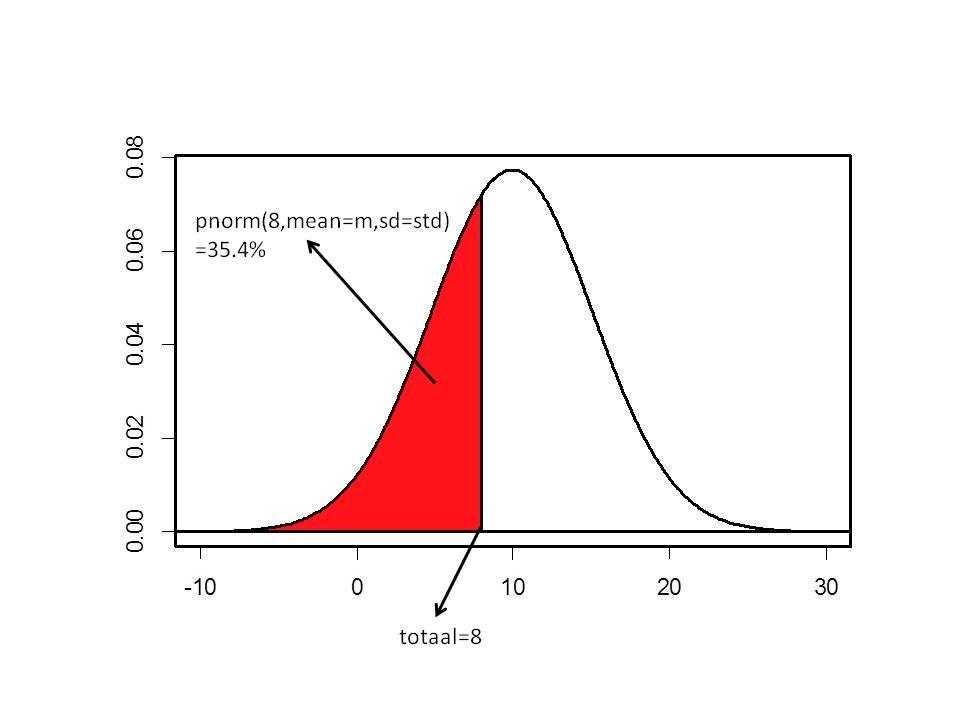
## [1] 9.931373
## [1] 5.155114

Als we er van uit kunnen gaan dat de studenten in de dataset een lukrake steekproef vormen, dan kunnen we deze normaal verdeling gebruiken om uitspraken te doen over de totale populatie van studenten die dit vak afleggen. Er kunnen percentielen en kwantielen berekend worden om vragen te beantwoorden zoals i) welk deel van de studentenpopulatie haalt 8/20 of minder? ii) wat zijn de scores van de 25% beste en 20% slechtste studenten? Voor de eerste vraag gaan we gebruik maken van een percentiel (zie hoger voor definitie).

## [1] 0.3539597

De functie pnorm berekent de oppervlakte onder de normale verdeling links van de score 8. Dit wordt ook weergegeven in onderstaande figuur:

De tweede vraag slaat niet op een percentiel, maar een kwantiel. Dit kan via de functie qnorm berekend worden. Zoals bij de pnorm functie gaat ook de functie qnorm de normale verdeling van de linker kant benaderen. De 20% slechtste studenten kan dus berekend worden als:

## [1] 5.592719

Dit betekent dus dat de 20% slechtste studenten een score halen die kleiner is dan 5.59. Dit vinden we ook op onderstaande figuur terug:

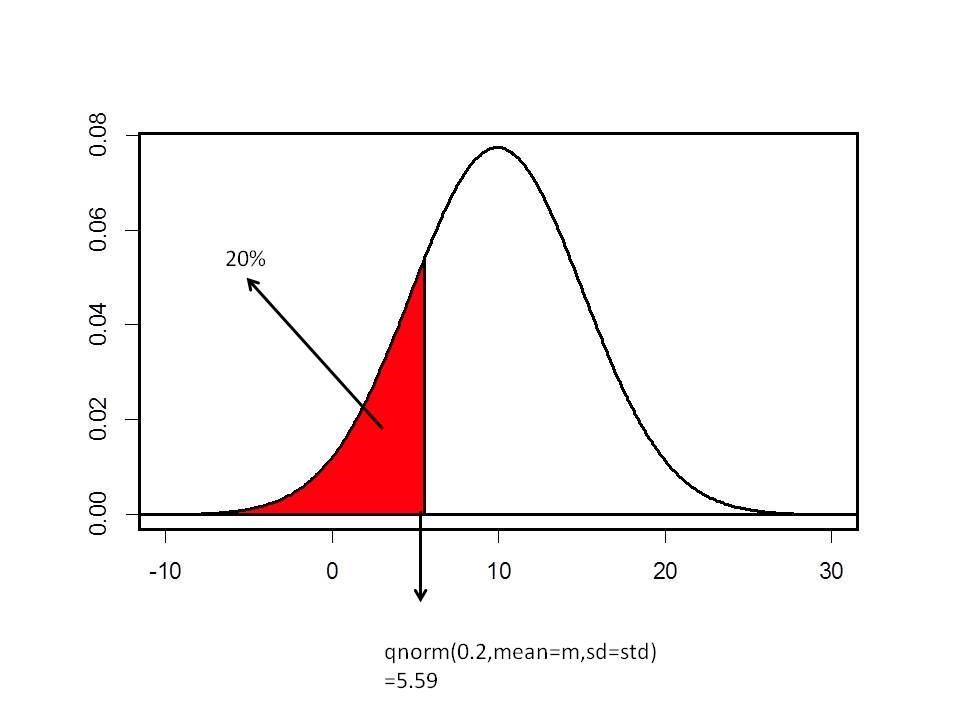
Om de score van de 25% beste studenten te berekenen moeten we het 100%-25%=75% kwantiel berekenen.

## [1] 13.40844

De 25% beste studenten halen een score van 13.4 of hoger:

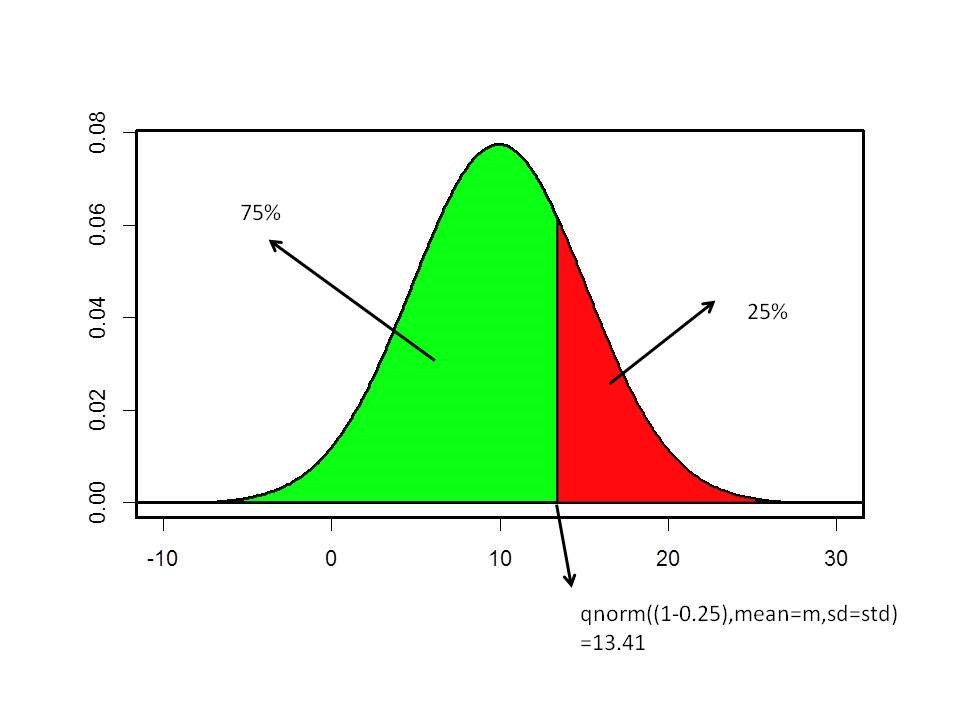
6.3 OEFENINGEN

  1. Herneem de oefening met de tonijngewichten. Op basis van deze dataset, welke proportie van de tonijnen in de Middellandse Zee zijn zwaarder dan 3 kg? Hoeveel wegen de zwaarste 3% van de tonijnen minstens?