Hoofdstuk 3 BESCHRIJVENDE STATISTIEK
Steekproefgegevens kunnen samengevat worden aan de hand van een aantal kengetallen of (beschrijvende) statistieken. In dit hoofdstuk worden de belangrijkste kengetallen voor ligging (centrum, locatie), spreiding en vorm (scheefheid en gepiektheid) besproken. Voor het benoemen van kengetallen of statistieken worden doorgaans Romeinse letters gebruikt. Indien de kengetallen berekend worden voor een volledige populatie of een gans proces, dan spreekt men van parameters in plaats van kengetallen of statistieken. Parameters worden voorgesteld door Griekse letters. Parameters zijn dus meestal niet gekend, maar worden geschat aan de hand van de kengetallen, dat we ook schatters kunnen noemen (deze worden soms ook voorgesteld door de Griekse letters met een ^ erop). Het aantal kengetallen dat zinvol berekend kan worden hangt af van de aard van de data. Voor nominale gegevens is de numerieke informatie eigenlijk beperkt tot de frequenties (met in het bijzonder de grootste frequentie). Voor ordinale gegevens kunnen we rekening houden met de ordening in de data en wordt het zinvol te spreken van, bijvoorbeeld, het middelste element van de steekproef. Bij intervalvariabelen en variabelen gemeten op een ratioschaal zal het rekenkundig gemiddelde een voorname rol spelen.
3.1 KENGETALLEN VAN CENTRALE LIGGING OF LOCATIE
Kengetallen van centrale ligging geven aan waar het centrum van de gegevens terug te vinden is. De meest gebruikte zijn de mediaan, de modus en het rekenkundig gemiddelde.
3.1.1 MEDIAAN
Op basis van de ordening van de data kan de mediaan bepaald worden voor zowel ordinale als kwantitatieve data. De mediaan (Me) van een verzameling gegevens is het middelste element van de geordende data. Bij een oneven aantal elementen wordt het gegeven door het \(\frac{n+1}{2}\) de element. Bij een even aantal elementen is de mediaan het gemiddelde van het \(\frac{n}{2}\) de en \(\frac{n+1}{2}\) de element. Als voorbeeld werken we verder met de dataset van de Olympische spelen. De mediaan van de leeftijd van de deelnemers is 26
## [1] 263.1.2 MODUS
Voor nominale data kunnen we enkel gebruik maken van de modus (\(M_0\)). Het is gedefinieerd als de waarneming met de hoogste frequentie. Zo telt atletiek het meeste aantal deelnemers met een medaille aan de Olympische spelen in onze dataset op basis van de tellingen uitgevoerd met de functie table().
De modus hoeft trouwens geen unieke oplossing te leveren. Het kan uiteraard voorkomen dat een aantal categorieën dezelfde frequentie hebben. Wanneer er in een frequentieverdeling 2 of meerdere pieken voorkomen spreekt men trouwens van een bimodaal of multimodaal patroon of verdeling.
3.1.3 REKENKUNDIG GEMIDDELDE
Het rekenkundig gemiddelde is veruit de best gekende maat voor de centrale ligging van een reeks waarnemingen. Het kan als volgt berekend worden:
\[\bar{x} = \frac{1}{n} \sum_{i=1}^{n}x_{i}\]
en in R toegepast worden met de functie mean().
## [1] 26.405433.2 KENGETALLEN VAN RELATIEVE LIGGING
Kengetallen van relatieve ligging geven de ligging van waarnemingen aan relatief ten opzichte van andere waarnemingen of kengetallen.
3.2.1 ORDESTATISTIEK, KWANTIEL EN PERCENTIEL
De i-de ordestatistiek of ordekengetal \(x_{(i)}\) in een steekproef van n waarnemingen is de i-de waarneming na rangschikking van de observaties van klein naar groot. Zo is de eerste ordestatistiek eveneens het minimum en de laatste of n-de ordestatistiek het maximum. Voor de leeftijden van medaillewinnaars vinden we 15 als laagste waarde en 61 als hoogste:
## [1] 15## [1] 61Door gebruik te maken van rechte haken en de sort functie om waarden te sorteren van klein naar groot kan bv. de 600-ste ordestatistiek van leeftijd als volgt opgeroepen worden:
## [1] 20Je kunt ook een reeks ordestatistieken op verschillende manieren oproepen in R:
## [1] 28 30 34Het (100×p)de steekproefpercentiel of –kwantiel \(c_p\), met 0<p<1, is een reëel getal dat groter is dan 100×p% van de waarnemingen en kleiner is dan 100×(1-p)% van de waarnemingen. De functie quantile() in R kan gebruikt worden om percentielen te bepalen:
## 2% 5% 12% 60%
## 18 19 21 273.2.2 KWARTIEL
Het eerste, tweede en derde kwartiel (\(Q_1\),\(Q_2\),\(Q_3\)) is het 25ste/50ste/75ste percentiel van de steekproef. De functie fivenum() geeft het minimum, maximum en het eerste, tweede en derde kwartiel. Merk op dat het tweede kwartiel gelijk is aan de mediaan.
## [1] 15 23 26 29 613.3 KENGETALLEN VAN SPREIDING
Kengetallen van spreiding geven een maat voor de spreiding van gegevens rond een centrale waarde. Gegevens die een zelfde gemiddelde (of ander kengetal voor centrale ligging) hebben kunnen sterk verschillen wat de spreiding van de gegevens betreft.
3.3.1 SPREIDINGSBREEDTE
De meest eenvoudige maat voor spreiding is de spreidingsbreedte (R). Dit is het verschil tussen het maximum en minimum. Je kunt het makkelijk manueel berekenen op basis van de resultaten uit de fivenum output, of gebruik maken van de functies max en min:
## [1] 46Een nadeel van deze maat is dat ze gebaseerd is op slechts 2 waarnemingen, en alle tussenliggende waarden geen invloed hebben. Het is erg afhankelijk van extreme waarden.
3.3.2 INTERKWARTIEL AFSTAND
Een beter beeld van spreiding kan bekomen worden door de kwartielen te gebruiken, meer bepaald de afstand tussen het eerste en derde kwartiel, de zgn. interkwartiel afstand (Q of IQR).
## [1] 6Aangezien de helft van de data tussen \(Q_1\) en \(Q_3\) liggen is deze maat van spreiding minder afhankelijk van extreme waarden.
3.3.3 GEMIDDELDE ABSOLUTE AFWIJKING
Zowel de spreidingsbreedte als de interkwartiel afstand kunnen beschouwd worden als spreidingsmaten rond de mediaan. Een maat voor spreiding rond het rekenkundige gemiddelde is de gemiddelde absolute afwijking of mean absolute deviation (MAD). Net zoals het rekenkundige gemiddelde is deze maat voor spreiding gevoelig voor extreme waarden (outliers).
## [1] 3.951355De interpretatie van deze waarde is dus dat gemiddeld, de leeftijd van een atleet ongeveer 4 jaar afwijkt van de gemiddelde leeftijd van alle atleten.
3.3.4 VARIANTIE
Voor gegevens gemeten op een ratio- of intervalschaal wordt vaak de variantie als maatstaf voor spreiding gebruikt. Voor een steekproef met n gegevens is de variantie gedefinieerd als:
\[\hat\sigma^2 = {\frac{\sum\limits_{i = 1}^N {\left( {x_i - \bar x} \right)^2 }} {(N-1)}}\]
In R is de functie var() beschikbaar om de steekproefvariantie te berekenen:
## [1] 26.031613.3.5 STANDAARDAFWIJKING
De standaardafwijking of standaarddeviatie is de vierkantswortel van de steekproefvariantie.
## [1] 5.102118## [1] 5.1021183.3.6 VARIATIECOEFFICIENT
Hoewel bovenstaande maten voor spreiding een belangrijke rol spelen in statistische analyses, zijn varianties en standaardafwijkingen vaak moeilijk te interpreteren. Neem het volgende voorbeeld, waarin twee datasets een verschillend gemiddelde maar gelijke variantie hebben.
dataset 1: 0,1,2,3,4,5,6,7,8,9,10
dataset 2: 100,101,102,103,104,105,106,107,108,109,110
## [1] 5## [1] 105## [1] 11## [1] 11Hier zou je intuïtief stellen dat de variatie in steekproef 2 relatief kleiner is dan die van steekproef 1. Met relatief bedoel je dan waarschijnlijk relatief ten opzichte van het gemiddelde. Zulke relatieve maat voor spreiding is de variatiecoëfficiënt, gedefinieerd als \(100× {\frac {\hat\sigma}{\bar x}}\). De standaarddeviatie wordt dus relatief ten opzichte van het gemiddelde geplaatst als een percentage. Voor bovenstaande twee datasets geeft dan het volgende resultaat:
## [1] 66.3325## [1] 3.15869En voor de leeftijd van de atleten:
## [1] 19.322233.4 KENGETALLEN VAN VORM
Hierboven werden een aantal kengetallen van centrale ligging en spreiding besproken. Naast de ligging van een frequentieverdeling en de breedte ervan, kan ook de vorm van verschillende frequentieverdelingen verschillen. We bespreken hier twee aspecten, namelijk scheefheid en gepiektheid.
3.4.1 SCHEEFHEID (SKEWNESS)
Histogrammen en stam-en-bladdiagrammen van steekproefgegevens kunnen symmetrisch of scheef zijn. Een histogram dat niet symmetrisch is wordt scheef genoemd. Bij een links scheef (of negatief scheef) histogram is de linkerstaart langer dan de rechterstaart. Bij een rechts scheef (of positief scheef) histogram is de rechterstaart langer dan de linkerstaart.
Bij een unimodaal histogram kan de scheefheid (skewness) bepaald worden aan de hand van de posities van het rekenkundig gemiddelde en de mediaan. Bij een perfect symmetrisch histogram zijn deze twee statistieken gelijk aan elkaar. Bij een links scheef histogram geldt dat het gemiddelde kleiner is dan de median (die op zijn beurt kleiner is dan de modus). Bij een rechts scheef histogram is de modus kleiner dan de mediaan, die zelf kleiner is dan het rekenkundig gemiddelde. De reden hiervoor is dat het rekenkundig gemiddelde gevoeliger is voor extreem grote of extreem kleine waarden dan de mediaan. Op basis hiervan leidde Pearson een scheefheidsmaatstaf af:
\[S_p = \frac {3(\bar x - M_e)}{\hat\sigma}\]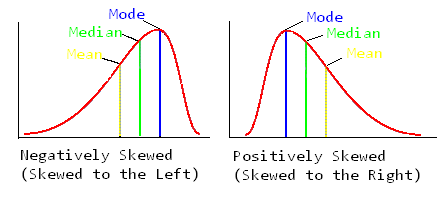
Deze maatstaf is steeds gelegen tussen -3 en 3, waarbij negatieve waarden wijzen op een links scheve verdeling, en positieve waren een rechts scheve verdeling. Voor de leeftijden van de atleten blijkt de verdeling licht rechts scheef te zijn.
## [1] 0.2383914Een tweede maat voor scheefheid is afgeleid van het derde centrale moment:
\[S=\frac{\sum\limits_{i = 1}^N {\left( {x_i - \bar x} \right)^3 }}{(N-1)\hat\sigma^3}\] Er bestaat in R (voor zover ik weet) geen functie of scheefheid te berekenen. Het is echter wel mogelijk om zelf functies in R te definiëren en die dan verder in je code en analyses toe te passen (het zelf definiëren van functies vraag ik zeker NIET op het examen). Laten we dit illustreren voor de scheefheid of skewness en vaststellen dat de verdeling van de leeftijd van de atleten opnieuw (en uiteraard) rechts scheef is:
#define function skew:
skew<-function(x){
sum((x-mean(x))^3)/((length(x)-1)*sd(x)^3)}
#use the function:
skew(Age)## [1] 0.85880763.4.2 GEPIEKTHEID (KURTOSIS)
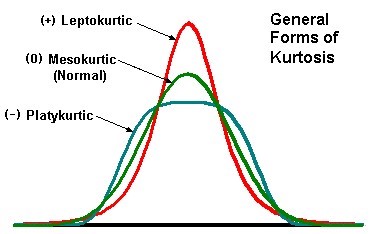
Gepiektheid is een maat voor de ‘scherpte’ van een verdeling. Als we een vergelijking maken met een normale verdeling (die we mesokurtisch noemen), zijn verdelingen die scherper zijn leptokurtisch, en plattere verdelingen platykurtisch.
De gepiektheid – die gelijk is aan nul voor normaal verdeelde data – kan als volgt berekend worden:
\[K=\frac{\sum\limits_{i = 1}^n {\left( {x_i - \bar x} \right)^4 }}{(N-1)\hat\sigma^4} - 3\] En ook hier kunnen we een functie schrijven in R om deze berekeningen uit te voeren en toe te passen op de leeftijden van de atleten. De positieve kurtosis wijst op een leptokurtische verdeling (dus meer gepiekt dan een normale verdeling):
## [1] 1.8022353.4.3 DE BOXPLOT
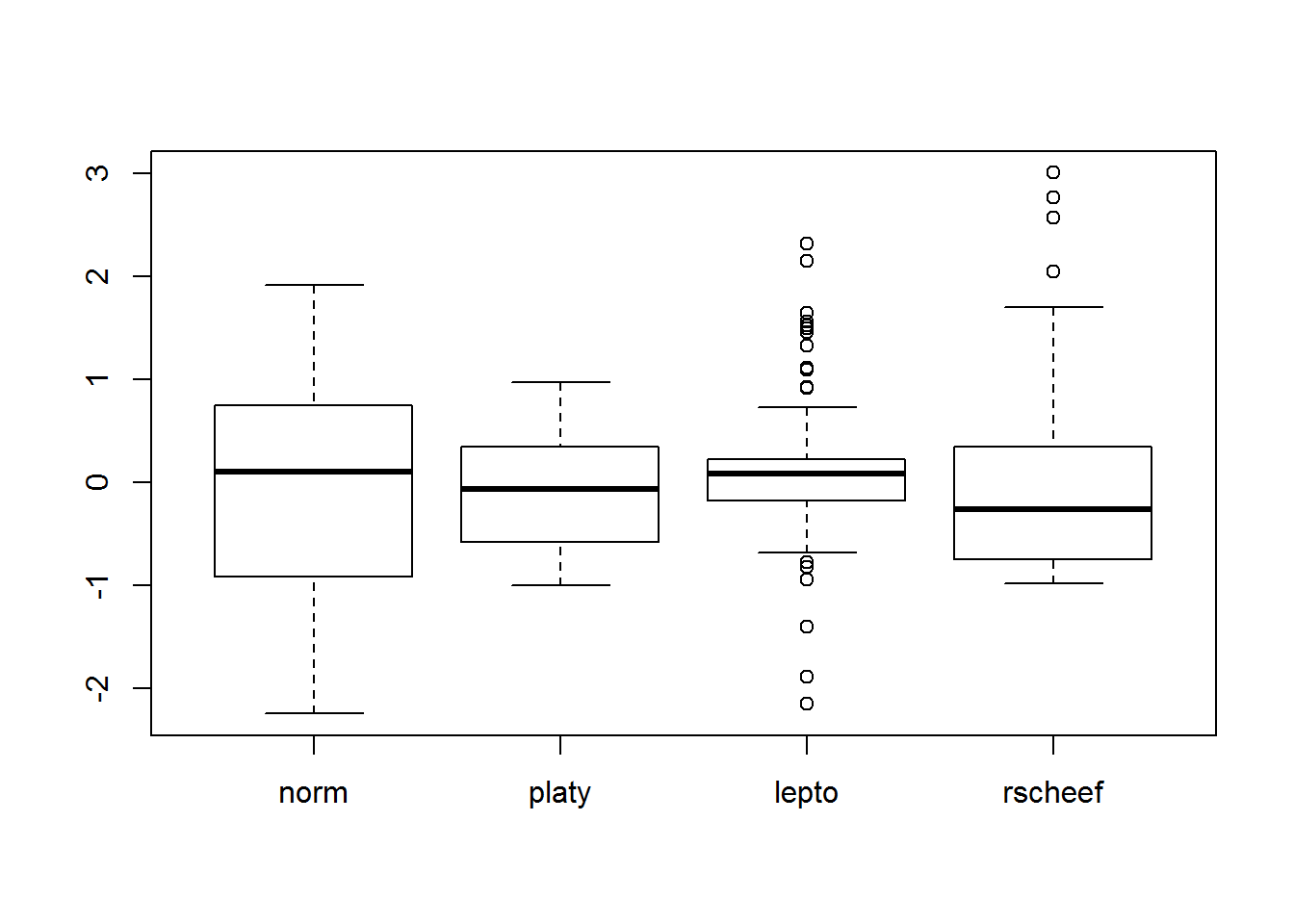
We hebben nu kennis gemaakt met verschillende kengetallen, die ons iets kunnen leren over de locatie, spreiding en vorm van een verdeling. Een soort van plot dat vaak gebruikt wordt om een samenvatting van de verdeling te geven, of te vergelijken tussen verschillende steekproeven is de boxplot. Deze wordt opgesteld gebruik makend van de vijf kengetallen die de functie fivenum functie berekent, namelijk het minimum, maximum en de drie kwartielen. In een eerste stap wordt de box gevormd door \(Q_1\) en \(Q_3\), en de mediaan (\(Q_2\)) wordt in de box aangegeven door een dikke lijn. Daarna worden de zgn. fences gevormd. Hiervoor worden eerst twee hypothetische grenzen berekend als \(Q_1-1.5*(Q_3-Q_1)\) en \(Q_3+1.5*(Q_3-Q_1)\). De meest extreme datapunten die nog wel binnen deze grenzen vallen worden gebruikt om de fences te tekenen. Punten die hier buiten vallen worden als (milde) outliers of uitschieters beschouwd. Niet alleen kan de ligging en spreiding gemakkelijk afgelezen worden van de boxplot, ook vormkenmerken en verschillen kunnen gemakkelijk gevisualiseerd worden. In onderstaande plot staan 4 boxplots. De meest linkse is normaal verdeeld (dus met scheefheid en gepiektheid gelijk aan nul). Daarnaast en in volgorde van links naar rechts staan boxplots van een platykurtische (negatieve kurtosis), leptokurtische (positieve kurtosis) en rechtsscheve (positieve skewness) verdeling. Deze kenmerken zijn respectievelijk vast te stellen aan de hand van relatief korte fences, relatief lange fences en fences met verschillende lengtes.
Wanneer we de boxplot van de leeftijden van de atleten bekijken dan merken we op dat de verdeling eerder licht rechtsscheef is, en dat deze scheefheid vooral te wijten is aan een beperkt aantal atleten van 38 jaar of ouder.
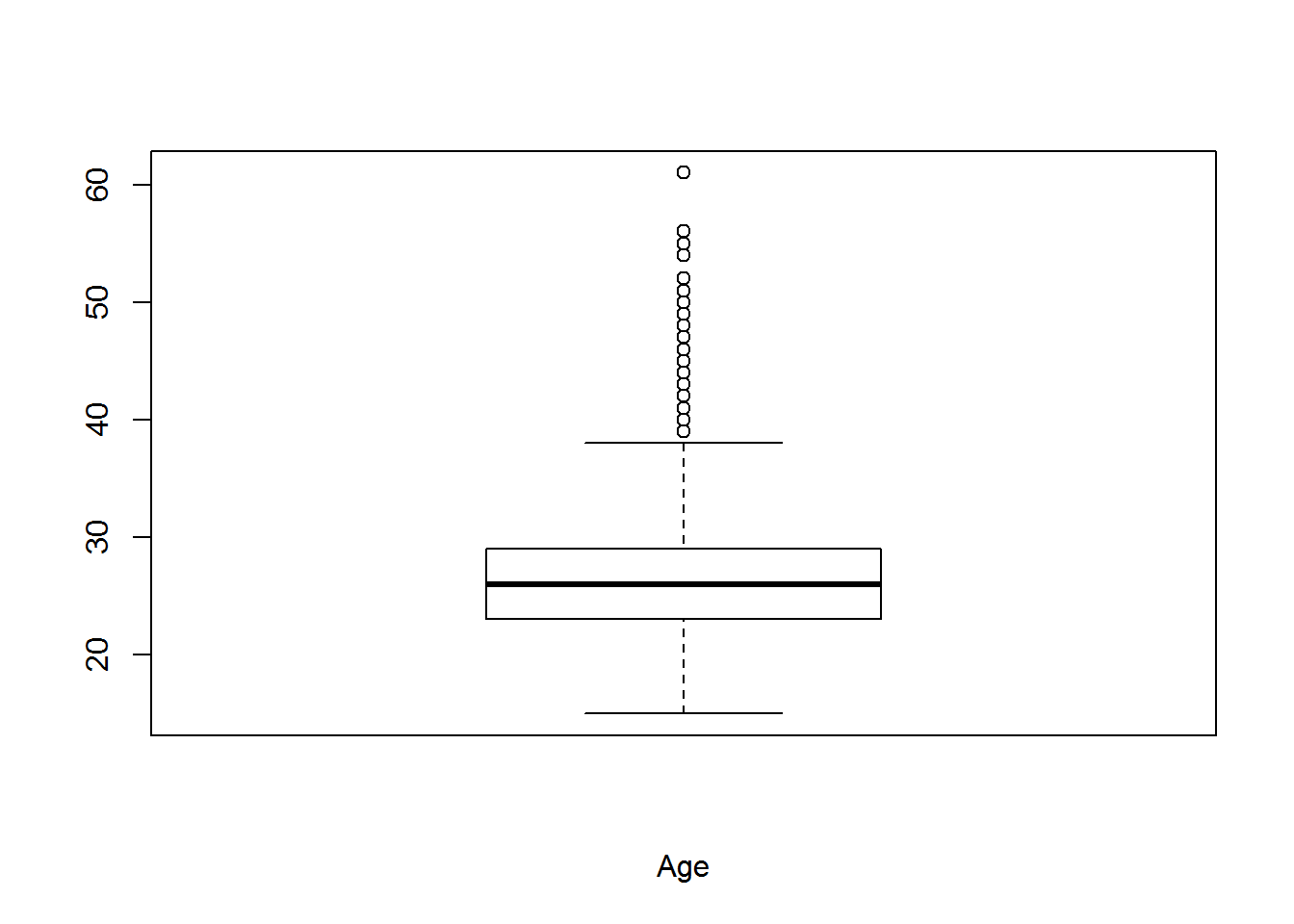
3.5 STANDARDISATIE VAN GEGEVENS EN DE Z-SCORE
Tal van variabelen kunnen in een waaier van verschillende eenheden uitgedrukt worden (bv. km vs mijlen; liter vs. gallons, ppm vs µg/ml). Ook zijn er mogelijk verschillende variabelen die een maat vormen voor eenzelfde biologisch fenomeen (bv. relatief gewicht, concentratie stress hormonen, fluctuerende asymmetrie). Wanneer we in zulke gevallen vergelijkingen willen maken is het noodzakelijk om alles op dezelfde noemer te brengen. Dit kan verwezenlijkt worden door de data \((x_i)\) te standaardiseren: \[Z_i = \frac{x_i-\bar x}{\hat\sigma}\] Van elke observatie wordt het steekproefgemiddelde afgetrokken en gedeeld door de standaarddeviatie. Het netto resultaat is dat de gegevens omgevormd zijn tot een dataset met gemiddelde gelijk aan nul en standaarddeviatie gelijk aan 1. Indien xi een normale verdeling volgt, zal zi de standaard normaal verdeling volgen. De zi worden ook Z-scores genoemd. Deze Z-scores geven aan hoeveel standaarddeviatie eenheden observaties van het gemiddelde verwijderd zijn, of met andere woorden hoe extreem ze zijn, ongeacht de eenheid waarin ze gemeten werden.
3.6 OEFENINGEN
- Bereken bovenstaande kengetallen voor de gewichten van 15 tonijnen gevangen in de Middellandse Zee. Wat is het 35% kwantiel? Ga grafisch na of de gegevens voldoen aan de normaliteits-assumptie (boxplot). De data zijn:
- Joris en Casper zijn beste maatjes. Op het einde van het schooljaar willen ze hun resultaten voor wiskunde vergelijken. Joris haalt bij meester X 74/100 en het klasgemiddelde is 69 met standaarddeviatie gelijk aan 12. Casper haalt 62/100 bij mevrouw Y en het klasgemiddelde bij hem is gelijk aan 59 met standaarddeviatie gelijk aan 5. Wie van de twee behaalde het beste resultaat? Welke belangrijke assumptie moet je hier maken om de resultaten van beide te kunnen maken?